前言

今天一樣主要為Writeup，解以下兩題，題目分別為求模反元素跟二次剩餘，開始吧!

Writeup

Modular Inverting (模反)

題目

網址 : https://cryptohack.org/courses/modular/mdiv/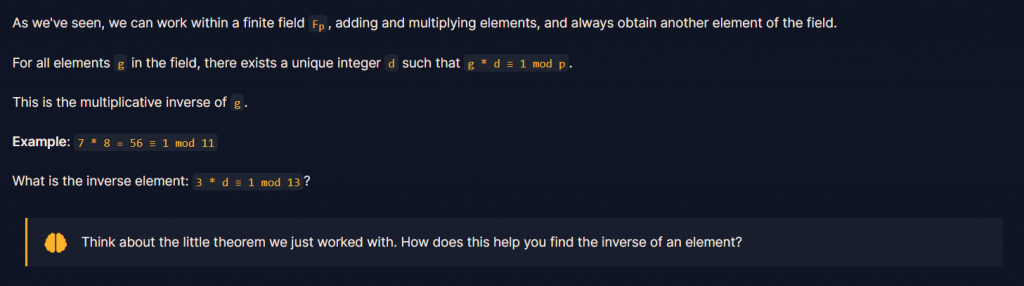

思路

題目為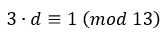，求d
因為3與13互質，所以可知d為3的模反元素

滿足公式

所以求出3的模反元素就ok惹

解法1

由上篇學到的費馬小定理推!(在p為質數的前提下才可使用)
先設3 = a, 13 = p, d = 1/a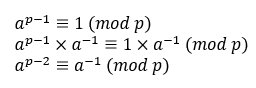

帶入數字得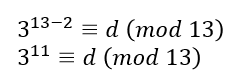

由此可知， d = 3^11 % 13

• code

print(3**11 % 13)

也可以利用pow()

pow(x, y, z)意思為 x^y % z

• code

print(pow(3, 11, 13))

解法2

利用Crypto.Util.number函式庫中的inverse可直接求出模反元素

要記得from Crypto.Util.number import inverse

• code

from Crypto.Util.number import inverse
print(inverse(3, 13))

• output
  

flag : 9

Writeup

Quadratic Residues (二次剩餘)

題目

網址 : https://cryptohack.org/courses/modular/root0/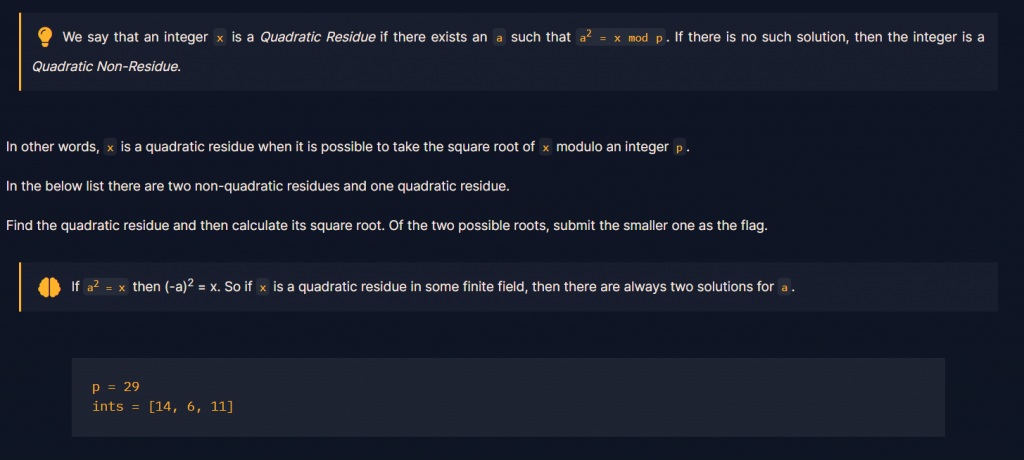

思路

當存在某個X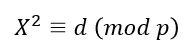， 成立時，稱d是模p的二次剩餘(quadratic residue)

反之不成立的話，稱d是模p的二次非剩餘(non-quadratic)

題目給了p跟3個數字，有兩個為二次非剩餘，一個為二次剩餘，我們不知道哪個是哪個，所以直接用迴圈測試
X的範圍為1~29，之後看X^2%p的結果是否為那三個數字其中一個，是的話就輸出
最後最小的為flag

解法

• code

list = [14, 6, 11]
#X^2 ≡ d mod p
#p = 29, d = someone_in_list

for X in range(1, 29):
    Quadratic_Residues = pow(X, 2, 29)
    if Quadratic_Residues in list :
        print(f"Quadratic_Residues: {Quadratic_Residues},square root: {X}")

• output
  

flag : 8

統整

• 模反元素(Modular Inverting)
  • 存在條件 : 整數a與模數n互質
  • 公式
    

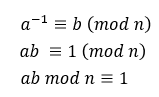
  b為a的模反元素

  • 求模反元素的方式(設整數 = a, 模數 = n, a的模反元素 = b)
    • Fermat's little theorem(限定模數要為質數，在此模數 = p)
      
      b = a^(p-2) % p
    • python Crypto.Util.number函式庫中的inverse

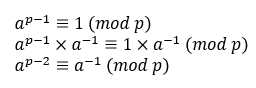
    from Crypto.Util.number import inverse
    b = inverse(a, n)
    

其他方式可自行查閱

• 二次剩餘(Quadratic residue)
  • 任意非零平方整數除以某個數後可能的餘數，我們稱之為「二次剩餘」
  • 
    • 成立時，稱d是模p的二次剩餘(quadratic residue)
    • 不成立，稱d是模p的二次非剩餘(non-quadratic)
  • 計算方式
    • X^2 % p = d
  • 例子!
    • mod 10(左邊為X，右邊為d(二次剩餘))
    • 

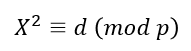
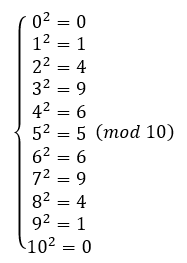
    1^1%10 = 1, 2^2%10 = 4, 3^2%10 = 9, 4^2%10 = 6, 5^2%10 = 5...

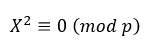    • 由此可知，對於模10而言，可能的餘數集合為{0, 1, 4, 5, 6, 9}，因為通常 都有解，所以不考慮0。所以在此，模10的二次剩餘為{1, 4, 5, 6, 9}

更詳細可自行查閱

小結

今天學了更深的模運算，模反元素跟二次剩餘，在查詢的過程中，也發現其實這些跟之後要學的加密有很大的關係，代表所以現在學的都為基礎QwQ(已經覺得小難惹)要再多花時間去熟悉這些定理/咚咚，加油!明天繼續解題

參考資料

模反元素 : https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E5%8F%8D%E5%85%83%E7%B4%A0
利用擴展歐幾里德求模反 : https://www.youtube.com/watch?v=fz1vxq5ts5I&t=41s&ab_channel=EmilyS
二次剩餘 : https://zh.wikipedia.org/zh-tw/%E4%BA%8C%E6%AC%A1%E5%89%A9%E4%BD%99
二次剩餘筆記 : http://gotonsb-numbertheory.blogspot.com/2014/04/quadratic-residues.html